Complete Electron Configuration for Zirconium (Zr, Zr4+)
Zirconium is the 40th element in the periodic table and its symbol is ‘Zr’. In this article, I have discussed in detail how to easily write the complete electron configuration of zirconium.
What is the electron configuration of zirconium?
The total number of electrons in zirconium is forty. These electrons are arranged according to specific rules in different orbitals.
The arrangement of electrons in zirconium in specific rules in different orbits and orbitals is called the electron configuration of zirconium.
The electron configuration of zirconium is [Kr] 4d2 5s2, if the electron arrangement is through orbitals. Electron configuration can be done in two ways.
- Electron configuration through orbit (Bohr principle)
- Electron configuration through orbital (Aufbau principle)
Electron configuration through orbitals follows different principles. For example Aufbau principle, Hund’s principle, and Pauli’s exclusion principle.
Zirconium atom electron configuration through orbit
Scientist Niels Bohr was the first to give an idea of the atom’s orbit. He provided a model of the atom in 1913. The complete idea of the orbit is given there.
The electrons of the atom revolve around the nucleus in a certain circular path. These circular paths are called orbit(shell). These orbits are expressed by n. [n = 1,2,3,4 . . . The serial number of the orbit]
K is the name of the first orbit, L is the second, M is the third, and N is the name of the fourth orbit. The electron holding capacity of each orbit is 2n2.
| Shell Number (n) | Shell Name | Electrons Holding Capacity (2n2) |
| 1 | K | 2 |
| 2 | L | 8 |
| 3 | M | 18 |
| 4 | N | 32 |
For example,
- n = 1 for K orbit.
The maximum electron holding capacity in K orbit is 2n2 = 2 × 12 = 2. - For L orbit, n = 2.
The maximum electron holding capacity in L orbit is 2n2 = 2 × 22 = 8. - n=3 for M orbit.
The maximum electron holding capacity in M orbit is 2n2 = 2 × 32 = 18. - n=4 for N orbit.
The maximum electron holding capacity in N orbit is 2n2 = 2 × 42 = 32.
Therefore, the maximum electron holding capacity in the first shell is two, the second shell is eight and the 3rd shell can have a maximum of eighteen electrons.
The atomic number is the number of electrons in that element. The atomic number of zirconium is 40. That is, the number of electrons in the zirconium is forty.
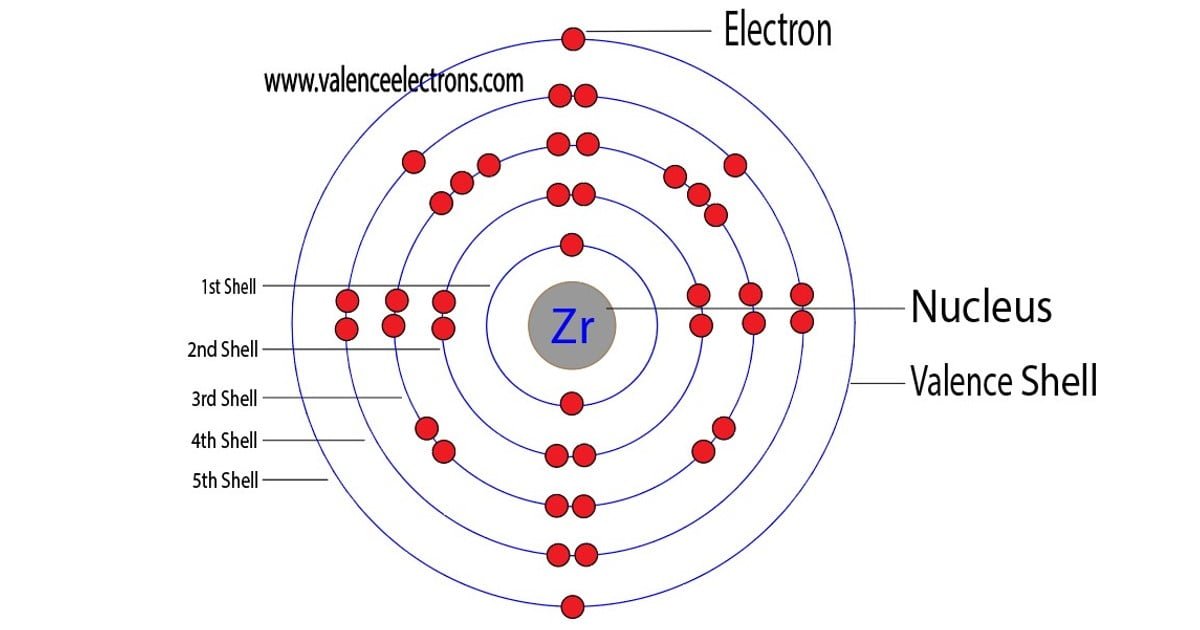
Therefore, a zirconium atom will have two electrons in the first shell, eight in the 2nd orbit, eighteen electrons in the 3rd shell, ten electrons in the 4th shell, and the remaining two electrons in the 5th shell.
Therefore, the order of the number of electrons in each shell of the zirconium(Zr) atom is 2, 8, 18, 10, 2. Electrons can be arranged correctly through orbits from elements 1 to 18.
The electron configuration of an element with an atomic number greater than 18 cannot be properly determined according to the Bohr atomic model. The electron configuration of all the elements can be done through the orbital diagram.
Electron configuration of zirconium through orbital
Atomic energy shells are subdivided into sub-energy levels. These sub-energy levels are also called orbital. The most probable region of electron rotation around the nucleus is called the orbital.
The sub-energy levels depend on the azimuthal quantum number. It is expressed by ‘l’. The value of ‘l’ is from 0 to (n – 1). The sub-energy levels are known as s, p, d, and f.
| Orbit Number | Value of ‘l’ | Number of subshells | Number of orbital | Subshell name | Electrons holding capacity | Electron configuration |
| 1 | 0 | 1 | 1 | 1s | 2 | 1s2 |
| 2 | 0 1 | 2 | 1 3 | 2s 2p | 2 6 | 2s2 2p6 |
| 3 | 0 1 2 | 3 | 1 3 5 | 3s 3p 3d | 2 6 10 | 3s2 3p6 3d10 |
| 4 | 0 1 2 3 | 4 | 1 3 5 7 | 4s 4p 4d 4f | 2 6 10 14 | 4s2 4p6 4d10 4f14 |
For example,
- If n = 1,
(n – 1) = (1–1) = 0
Therefore, the value of ‘l’ is 0. So, the sub-energy level is 1s. - If n = 2,
(n – 1) = (2–1) = 1.
Therefore, the value of ‘l’ is 0, 1. So, the sub-energy levels are 2s, and 2p. - If n = 3,
(n – 1) = (3–1) = 2.
Therefore, the value of ‘l’ is 0, 1, 2. So, the sub-energy levels are 3s, 3p, and 3d. - If n = 4,
(n – 1) = (4–1) = 3
Therefore, the value of ‘l’ is 0, 1, 2, 3. So, the sub-energy levels are 4s, 4p, 4d, and 4f. - If n = 5,
(n – 1) = (n – 5) = 4.
Therefore, l = 0,1,2,3,4. The number of sub-shells will be 5 but 4s, 4p, 4d, and 4f in these four subshells it is possible to arrange the electrons of all the elements of the periodic table.
| Subshell name | Name source | Value of ‘l’ | Value of ‘m’ (0 to ± l) | Number of orbital (2l+1) | Electrons holding capacity 2(2l+1) |
| s | Sharp | 0 | 0 | 1 | 2 |
| p | Principal | 1 | −1, 0, +1 | 3 | 6 |
| d | Diffuse | 2 | −2, −1, 0, +1, +2 | 5 | 10 |
| f | Fundamental | 3 | −3, −2, −1, 0, +1, +2, +3 | 7 | 14 |
The orbital number of the s-subshell is one, three in the p-subshell, five in the d-subshell and seven in the f-subshell. Each orbital can have a maximum of two electrons.
The sub-energy level ‘s’ can hold a maximum of two electrons, ‘p’ can hold a maximum of six electrons, ‘d’ can hold a maximum of ten electrons, and ‘f’ can hold a maximum of fourteen electrons.

Aufbau is a German word, which means building up. The main proponents of this principle are scientists Niels Bohr and Pauli. The Aufbau method is to do electron configuration through the sub-energy level.
The Aufbau principle is that the electrons present in the atom will first complete the lowest energy orbital and then gradually continue to complete the higher energy orbital.
The energy of an orbital is calculated from the value of the principal quantum number ‘n’ and the azimuthal quantum number ‘l’. The orbital for which the value of (n + l) is lower is the low energy orbital and the electron will enter that orbital first.
| Orbital | Orbit (n) | Azimuthal quantum number (l) | Orbital energy (n + l) |
| 3d | 3 | 2 | 5 |
| 4s | 4 | 0 | 4 |
Here, the energy of 4s orbital is less than that of 3d. So, the electron will enter the 4s orbital first and enter the 3d orbital when the 4s orbital is full. The method of entering electrons into orbitals through the Aufbau principle is 1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 5f 6d.
The first two electrons of zirconium enter the 1s orbital. The s-orbital can have a maximum of two electrons. Therefore, the next two electrons enter the 2s orbital.
The p-orbital can have a maximum of six electrons. So, the next six electrons enter the 2p orbital. The second orbit is now full. So, the remaining electrons will enter the third orbit.
Then two electrons will enter the 3s orbital and the next six electrons will be in the 3p orbital of the third orbit. The 3p orbital is now full. So, the next two electrons will enter the 4s orbital and ten electrons will enter the 3d orbital.
The 3d orbital is now full. So, the next six electrons enter the 4p orbital. The 4p orbital is now full. Then the next two electrons will enter the 5s orbital. The 5s orbital is now full.
So the remaining two electrons enter the 4d orbital. Therefore, the zirconium complete electron configuration will be 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d2 5s2.

Note: The unabbreviated electron configuration of zirconium is [Kr] 4d2 5s2. When writing an electron configuration, you have to write serially.
Zirconium ion(Zr4+) electron configuration
The ground state electron configuration of zirconium is 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d2 5s2.
This electron configuration shows that the last shell of zirconium has two electrons and the d-orbital has a total of two electrons. Therefore, the valence electrons of zirconium are four.
The elements that have 1, 2, or 3 electrons in the last shell donate the electrons in the last shell during bond formation. The elements that form bonds by donating electrons are called cations.
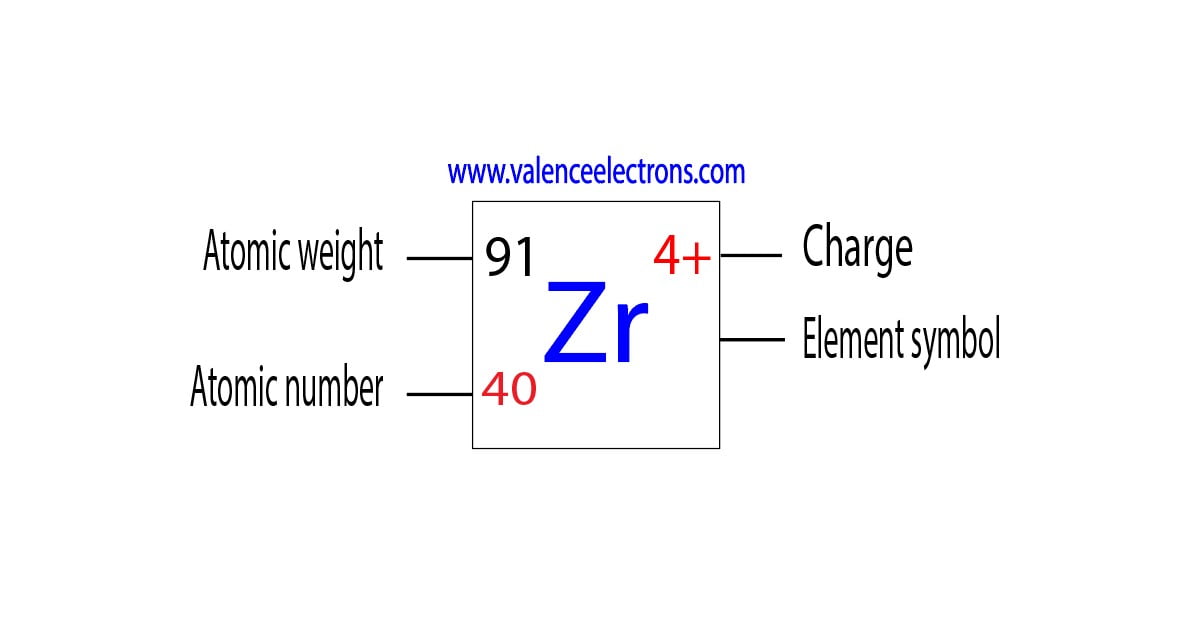
During the formation of a bond, zirconium donates two electrons of the last shell and two electrons of the 4d orbital to form bonds and turns into a zirconium ion(Zr4+). That is, zirconium is a cation element.
Zr – 4e– → Zr4+
The electron configuration of zirconium ion(Zr4+) is 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6. The electron configuration shows that the zirconium ion(Zr4+) has four shells and the last shell has eight electrons.
This electron configuration shows that the zirconium ion has acquired electron configuration of krypton and it achieves an octave full stable electron configuration.
Video for Write the Electron Configuration for Zirconium (Zr)
FAQs
How do you write the complete electron configuration for zirconium?
Ans: The complete electron configuration for zirconium is 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d2 5s2.
What is the unabbreviated electron configuration of zirconium?
The unabbreviated electron configuration of zirconium is [Kr] 4d2 5s2.
How many unpaired electrons does Zr4+ have?
Zirconium in its +4 oxidation state (Zr4+) has zero unpaired electrons. The 4+ charge indicates that Zirconium has lost four electrons, leaving behind a configuration of [Kr] 4d0 5s0, where all the electrons are paired.
What is the ground state electron configuration for Zr?
The ground state electron configuration of zirconium is 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d2 5s2. This electron configuration shows that the last shell of zirconium has two electrons and the d-orbital has two electrons.
What is the valency of zirconium?
The valency of zirconium is 4.
How many electrons are in the third energy level for zirconium(Zr)?
18 electrons. A zirconium atom has two electrons in the first shell, eight in the 2nd orbit, eighteen electrons in the 3rd shell, ten electrons in the 4th shell, and the remaining two electrons in the 5th shell.
How many unpaired electrons does Zr have?
Zirconium has two unpaired electrons. The electron configuration of zirconium is [Kr] 4d2 5s2. In the 4d subshell, there are two electrons in separate orbitals, which are unpaired. Therefore, Zirconium has two unpaired electrons.