How to Write the Electron Configuration for Germanium (Ge)?
Germanium is the 32th element in the periodic table and the symbol is ‘Ge’. Germanium has an atomic number of 32, which means that its atom has 32 electrons around its nucleus.
To write the electron configuration for germanium, the first two electrons enter the 1s orbital. Since the 1s orbital can hold only two electrons the next two will enter the 2s orbital. The next six electrons enter the 2p subshell. The p subshell can hold a maximum of six electrons. So first we put six electrons in the 2p subshell and then the next two electrons in the 3s orbital.
Since the 3s is now full, the electrons will move to the 3p subshell, where the next six electrons will enter. The 3p subshell is now full. Consequently, the following two electrons will enter the 4s orbital. Since the 4s orbital is full, the next ten electrons will move into the 3d subshell. The 3d subshell is now full. Consequently, the remaining two electrons will enter the 4p subshell. Hence, the electron configuration of germanium will be 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p2.
The electron configuration of germanium refers to the arrangement of electrons in the germanium atom’s orbitals. It describes how electrons are distributed among the various atomic orbitals and energy levels, and provides a detailed map of where each electron is likely to be found.
To understand the mechanism of germanium electron configuration, you need to understand two basic things. These are orbits and orbitals. Also, you can arrange electrons in those two ways. In this article, I have discussed all the necessary points to understand the mechanism of germanium electron configuration. I hope this will be helpful in your study.
Electron arrangement of Germanium through orbit
Scientist Niels Bohr was the first to give an idea of the atom’s orbit. He provided a model of the atom in 1913 and provided a complete idea of orbit in that model.
The electrons of the atom revolve around the nucleus in a certain circular path. These circular paths are called orbits (shells or energy levels). These orbits are expressed by n. [n = 1,2,3,4 . . . The serial number of the orbit]
The name of the first orbit is K, L is the second, M is the third, and N is the name of the fourth orbit. The electron holding capacity of each orbit is 2n2.
| Shell Number (n) | Shell Name | Electrons Holding Capacity (2n2) |
| 1 | K | 2 |
| 2 | L | 8 |
| 3 | M | 18 |
| 4 | N | 32 |
Explanation:
- Let, n = 1 for K orbit. So, the maximum electron holding capacity in the K orbit is 2n2 = 2 × 12 = 2 electrons.
- n = 2, for L orbit. The maximum electron holding capacity in the L orbit is 2n2 = 2 × 22 = 8 electrons.
- n=3 for M orbit. The maximum electron holding capacity in the M orbit is 2n2 = 2 × 32 = 18 electrons.
- n=4 for N orbit. The maximum electron holding capacity in N orbit is 2n2 = 2 × 42 = 32 electrons.
Therefore, the maximum electron holding capacity in the first shell is two, the second shell is eight and the 3rd shell can have a maximum of eighteen electrons.
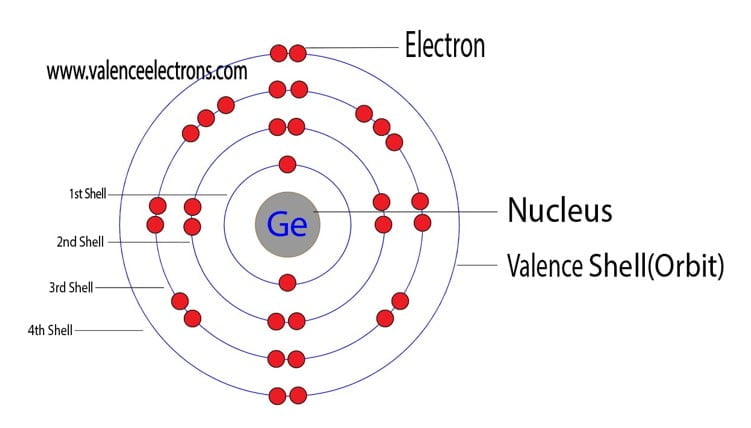
The atomic number is the number of electrons in that element. The atomic number of germanium is 32. That is, the number of electrons in germanium is thirty-two. Therefore, the germanium atom will have two electrons in the first shell, eight in the 2nd orbit, eighteen electrons in the 3rd shell, and the remaining four electrons will be in the fourth shell. Therefore, the order of the number of electrons in each shell of the germanium atom is 2, 8, 18, 4.
The Bohr atomic model has many limitations. In the Bohr atomic model, the electrons can only be arranged in different shells but the exact position, orbital shape, and spin of the electron cannot be determined.
Also, electrons can be arranged correctly from 1 to 18 elements. The electron arrangement of any element with atomic number greater than 18 cannot be accurately determined by the Bohr atomic model following the 2n2 formula. We can overcome all limitations of the Bohr model following the electron configuration through orbital.
Electron configuration of Germanium through orbital
Atomic energy shells are subdivided into sub-energy levels. These sub-energy levels are also called orbital. The most probable region of electron rotation around the nucleus is called the orbital.
The sub-energy levels depend on the azimuthal quantum number. It is expressed by ‘l’. The value of ‘l’ is from 0 to (n – 1). The sub-energy levels are known as s, p, d, and f.
| Orbit Number | Value of ‘l’ | Number of subshells | Number of orbitals | Subshell name | Electrons holding capacity | Electron configuration |
| 1 | 0 | 1 | 1 | 1s | 2 | 1s2 |
| 2 | 0 1 | 2 | 1 3 | 2s 2p | 2 6 | 2s2 2p6 |
| 3 | 0 1 2 | 3 | 1 3 5 | 3s 3p 3d | 2 6 10 | 3s2 3p6 3d10 |
| 4 | 0 1 2 3 | 4 | 1 3 5 7 | 4s 4p 4d 4f | 2 6 10 14 | 4s2 4p6 4d10 4f14 |
Explanation:
- If n = 1,
(n – 1) = (1–1) = 0
Therefore, the value of ‘l’ is 0. So, the sub-energy level is 1s. - If n = 2,
(n – 1) = (2–1) = 1.
Therefore, the value of ‘l’ is 0, 1. So, the sub-energy levels are 2s, and 2p. - If n = 3,
(n – 1) = (3–1) = 2.
Therefore, the value of ‘l’ is 0, 1, 2. So, the sub-energy levels are 3s, 3p, and 3d. - If n = 4,
(n – 1) = (4–1) = 3
Therefore, the value of ‘l’ is 0, 1, 2, 3. So, the sub-energy levels are 4s, 4p, 4d, and 4f. - If n = 5,
(n – 1) = (n – 5) = 4.
Therefore, l = 0,1,2,3,4. The number of sub-shells will be 5 but 4s, 4p, 4d, and 4f in these four subshells it is possible to arrange the electrons of all the elements of the periodic table.
| Sub-shell name | Name source | Value of ‘l’ | Value of ‘m’ (0 to ± l) | Number of orbital (2l+1) | Electrons holding capacity 2(2l+1) |
| s | Sharp | 0 | 0 | 1 | 2 |
| p | Principal | 1 | −1, 0, +1 | 3 | 6 |
| d | Diffuse | 2 | −2, −1, 0, +1, +2 | 5 | 10 |
| f | Fundamental | 3 | −3, −2, −1, 0, +1, +2, +3 | 7 | 14 |
The orbital number of the s-subshell is one, three in the p-subshell, five in the d-subshell, and seven in the f-subshell. Each orbital can have a maximum of two electrons.
The sub-energy level ‘s’ can hold a maximum of two electrons, ‘p’ can hold a maximum of six electrons, ‘d’ can hold a maximum of ten electrons, and ‘f’ can hold a maximum of fourteen electrons.
Aufbau is a German word, which means building up. The main proponents of this principle are scientists Niels Bohr and Pauli. The Aufbau method is to do electron configuration through the sub-energy level.
The Aufbau principle is that the electrons present in the atom will first complete the lowest energy orbital and then gradually continue to complete the higher energy orbital.
The energy of an orbital is calculated from the value of the principal quantum number ‘n’ and the azimuthal quantum number ‘l’. The orbital for which the value of (n + l) is lower is the low energy orbital and the electron will enter that orbital first.
| Orbital | Orbit (n) | Azimuthal quantum number (l) | Orbital energy (n + l) |
| 3d | 3 | 2 | 5 |
| 4s | 4 | 0 | 4 |
Here, the energy of 4s orbital is less than that of 3d. So, the electron will enter the 4s orbital first and enter the 3d orbital when the 4s orbital is full.
Following the Aufbau principle, the sequence of entry of electrons into orbitals is 1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s 5f 6d 7p.
Therefore, the complete electron configuration for germanium should be written as 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p2.
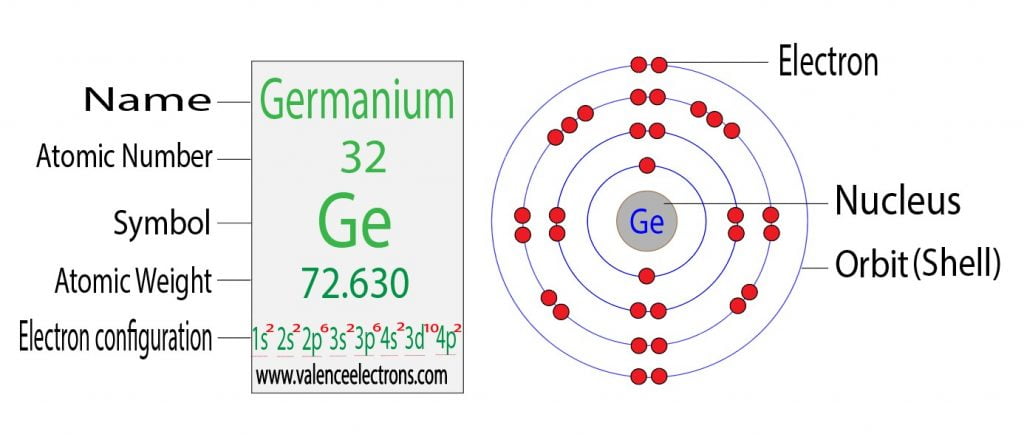
Note: The abbreviated electron configuration of germanium is [Ar] 3d10 4s2 4p2. When writing an electron configuration, you have to write serially.
Germanium excited state electron configuration
Atoms can jump from one orbital to another orbital in an excited state. This is called quantum jump. The ground state electron configuration of germanium is 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p2. In the germanium ground-state electron configuration, the last two electrons of the 4p orbital are located in the 4px and 4py orbitals.
We already know that the p-subshell has three orbitals. The orbitals are px, py, and pz and each orbital can have a maximum of two electrons. Then the correct electron configuration of germanium in the ground state will be 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4px1 4py1.
This electron configuration shows that the last shell of the germanium atom has two unpaired electrons. So in this case, the valency of germanium is 2.
When the germanium atom is excited, then the germanium atom absorbs energy. As a result, an electron in the 4s orbital jumps to the 4pz orbital. Therefore, the electron configuration of germanium(Ge*) in an excited state will be 1s2 2s2 2p6 3s2 3p6 3d10 4s1 4px1 4py1 4pz1.
The valency of the element is determined by electron configuration in the excited state. Here, germanium has four unpaired electrons. So, the valency of germanium is 4.
Germanium ion(Ge2+, Ge4+) electron configuration
The electron configuration shows that the last shell of germanium has four electrons. Therefore, the valence electrons of germanium are four. There are two types of germanium ions. The germanium atom exhibits Ge2+ and Ge4+ ions. The germanium atom donates two electrons in the 4p orbital to form a germanium ion(Ge2+).
Ge – 2e– → Ge2+
Here, the electron configuration of germanium ion(Ge2+) is 1s2 2s2 2p6 3s2 3p6 3d10 4s2. On the other hand, the germanium atom donates two electrons in 4p orbital and two electrons in the 4s orbital to convert germanium ion(Ge4+).
Ge – 4e– → Ge4+
Here, the electron configuration of the germanium ion(Ge4+) is 1s2 2s2 2p6 3s2 3p6 3d10. Germanium atoms exhibit +2 and +4 oxidation states. The oxidation state of the element changes depending on the bond formation.